- Home
- 割り算(変動法)でのスタート位置と答えの見方
割り算(変動法)でのスタート位置と答えの見方
割り算(変動法)でのスタート位置と答えの見方
割り算の計算を始める前に、スタート位置と、答えの見方の説明をします。
割り算のやり方もたくさんありますが、個人的におすすめなやり方が変動法です。
変動法とは、私が勝手に作った言葉です。
答えの一の位がいつも変動することから、この呼び方を付けました。
この変動法でのいいところは、小数でも同様の方法で計算が導けることです。
わざわざ小数だからとやり方を変える必要がありません。
定位法のやり方は別のページの記載しますので興味のある方はそちらをご覧ください。
- そろばんに割られる数を置きます。
- 割る数の桁に左手人差し指を置きます
- 置いた左手人差し指を左に2つ移動させます
- 計算が終わったら、答えを読み取ります
そのまま左手人差し指は答えを書くまで動かしません
左手人差し指が一の位です。それを読み取り答えとします。
369÷3のスタート位置と答えの見方練習
369÷3=123を例にとって、スタート位置と答えの見方を説明します。
(計算方法は別ページ参照)
- そろばんに割られる数を置きます
- 割る数の桁に左手人差し指を置きます
- 置いた左手人差し指を左に2つ移動させます
- 計算が終わったら、答えを読み取ります
そろばんに割られる数である369を置きます
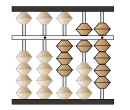
割る数は3つまり1ケタです
ここに左手人差し指を置きます。
※すでに置いた割られる数に関係はありません
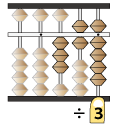
この状態で計算を始めます
そのまま左手人差し指は答えを書くまで動かしません
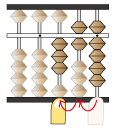
計算を行うと、下図のようになります(計算方法は別ページにて)

左手人差し指が一の位です。それを読み取り答えとします。
答えが123となります
60,984÷24のスタート位置と答えの見方練習
60,984÷24=2,541を例にとって、スタート位置と答えの見方を説明します。
(計算方法は別ページ参照)
- そろばんに割られる数を置きます
- 割る数の桁に左手人差し指を置きます
- 置いた左手人差し指を左に2つ移動させます
- 計算が終わったら 、答えを読み取ります
そろばんに割られる数である60,984を置きます

割る数は24つまり2ケタです
ここに左手人差し指を置きます。
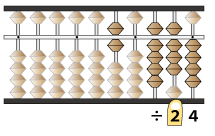
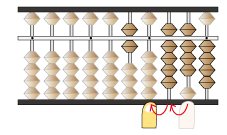
この状態で計算を始めます
そのまま左手人差し指は答えを書くまで動かしません
計算を行うと、下図のようになります(計算方法は別ページにて)
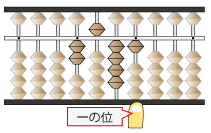
左手人差し指が一の位です。それを読み取り答えとします。
答えが2,541となります
0.25÷5のスタート位置と答えの見方練習
この変動法でのいいところは、小数でも同様の方法で計算が導けることです。
わざわざ小数だからとやり方を変える必要がありません。
0.25÷5=0.05を例にとって、スタート位置と答えの見方を説明します。
(計算方法は別ページ参照)
- そろばんに割られる数を置きます
- 割る数の桁に左手人差し指を置きます
- 置いた左手人差し指を左に2つ移動させます
- 計算が終わったら、答えを読み取ります
そろばんに割られる数である0.25を 置きます
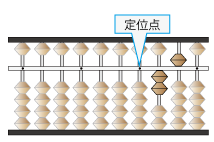
割る数は5つまり1ケタです
ここに左手人差し指を置きます。
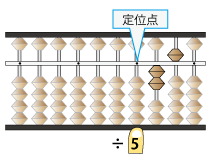
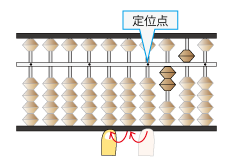
この状態で計算を始めます
そのまま左手人差し指は答えを書くまで動かしません
計算を行うと、下図のようになります(計算方法は別ページにて)
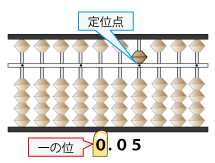
左手人差し指が一の位です。それを読み取り答えとします。
答えが0.05となります
0.042÷0.0007のスタート位置と答えの見方練習
0.042÷0.0007=60を例にとって、スタート位置と答えの見方を説明します。
(計算方法は別ページ参照)
- そろばんに割られる数を置きます
- 割る数の桁に左手人差し指を置きます
- 置いた左手人差し指を左に2つ移動させます
- 計算が終わったら、答えを読み取ります
そろばんに割られる数である0.042を置きます
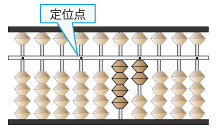
割る数は0.0007つまり小数第4位です
ここに左手人差し指を置きます。
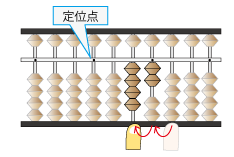
この状態で計算を始めます
そのまま左手人差し指は答えを書くまで動かしません
計算を行うと、下図のようになります(計算方法は別ページにて)
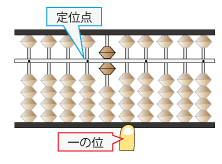
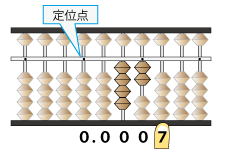
左手人差し指が一の位です。それを読み取り答えとします。
答えが60となります
【割り算①やり方|3桁÷1桁】次のページへ

